Repéré au matin du samedi 22 mai 2010 dans un champ du Wiltshire au sud-est de Marloborough, ce crop circle m’avait captivé par sa géométrie particulière. Ce week-end de Pentecôte 2010 allait me donner le temps nécessaire pour formuler un postulat de lecture.
Dans les semaines qui suivirent, l’hypothèse formulée par Richard Andrews finit par s’imposer. Ses conclusions faisaient du Crop Circle de Milton Windmill l’expression d’une formule du mathématicien suisse Leonhard Euler, bien que – du propre aveu de Richard – cette formule ne soit pas exactement répliquée par l’encodage supposé en langage ASCII de la figure.
Sa conclusion me laissait pour le moins sceptique, mes recherches sur l’architecture sacrée m’ayant appris à me méfier des approximations : Une formulation est juste ou elle ne l’est pas. Je comprenais mal d’autre part les raisons qui auraient motivé les auteurs de ce Crop Circle à encoder un message en ASCII; la géométrie et les mathématiques sont des langages universels, ce qui n’est certainement pas le cas de cette vieille norme de codage américain de caractères en informatique normalisé pour l’échange d’information (ASCII). Pourtant, même Lucy Pringle – figure passionnée du milieu – ne voulu rien entendre d’autre…
La composition générale de ce Crop Circle évoque un gâteau divisé en 12 tranches égales qui s’articulent autour d’un rond central. On dénombre 8 cercles intermédiaires entre le rond central et le périmètre extérieur, matérialisés par des fragments d’arcs apparaissant sur leurs périmètres respectifs.
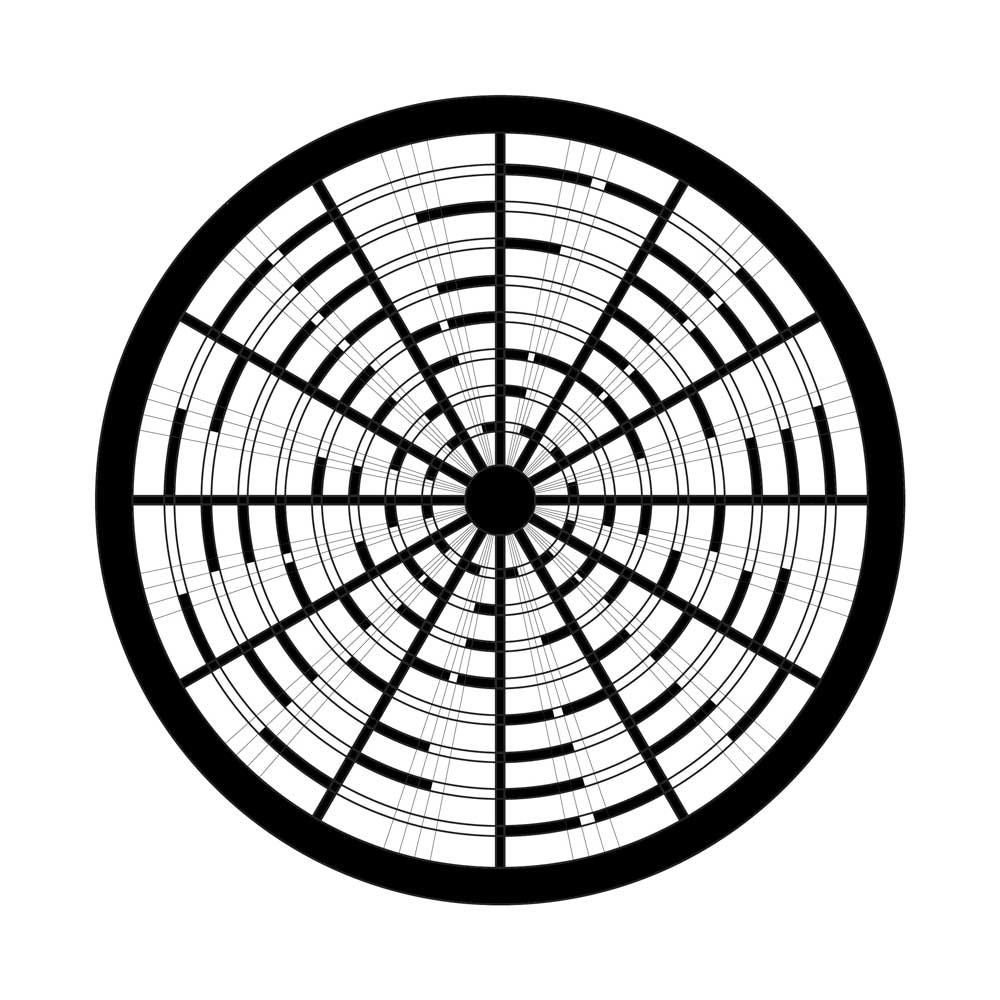
Richard Andrews a utilisé les rayons de ces divisions pour extraire son code binaire. Mon attention s’est portée à l’inverse sur la disposition des fragments d’arc dans chacune des tranches, car elle constitue un code non plus binaire mais quaternaire dans la mesure où chaque arc de cercle peut présenter l’une des quatre configurations suivantes : Une fraction d’arc accolé à la gauche de la tranche [1 0], une fraction d’arc accolé à la droite [0 1], deux fractions accolées de part et d’autre de la tranche [1 1] et enfin l’absence de fraction qui constitue la quatrième variante [0 0].
En substituant les chiffres 1, 2, 3 à ces différents cas de figures – l’absence de fraction [0 0] n’étant pas indiquée – on obtient une représentation plus synthétique de l’ensemble :
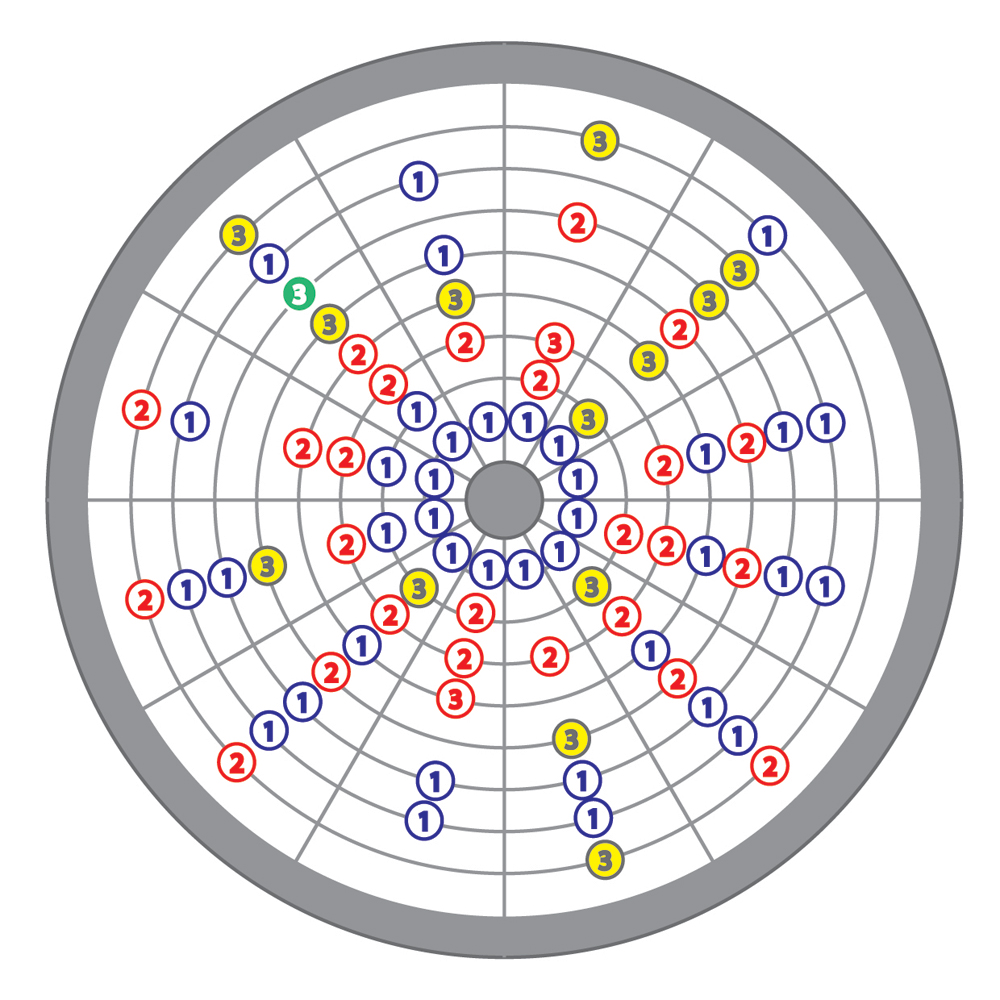
On remarque ainsi que – sur le périmètre d’un même cercle – le chiffre 3 est systématiquement adjacent aux chiffres 1 et 2, alors que les chiffres 1 et 2 ne le sont jamais l’un avec l’autre, ce qui laisse supposer qu’ils sont de nature polaire ou opposée. Ce postulat est renforcé par leur disposition respective autour du chiffre 3 : En tournant dans le sens des aiguilles d’une montre, les chiffres 2 précèdent toujours un 3, alors que les chiffres 1 le suivent.
Exprimé différemment, le chiffre 3 [1 1] désigne un élément en mouvement dont l’amplitude et le sens de rotation sont caractérisés par les chiffres 1 [1 0] et 2 [0 1].
A une exception près : L’un des chiffres 3 [1 1] figure seul – signalé en vert ci-dessous – sur le 6e cercle intermédiaire en partant du centre. Nous retrouvons ici un artifice souvent utilisé par les bâtisseurs pour attirer notre attention sur un détail qui fournit un élément de lecture important. Nous y reviendrons.
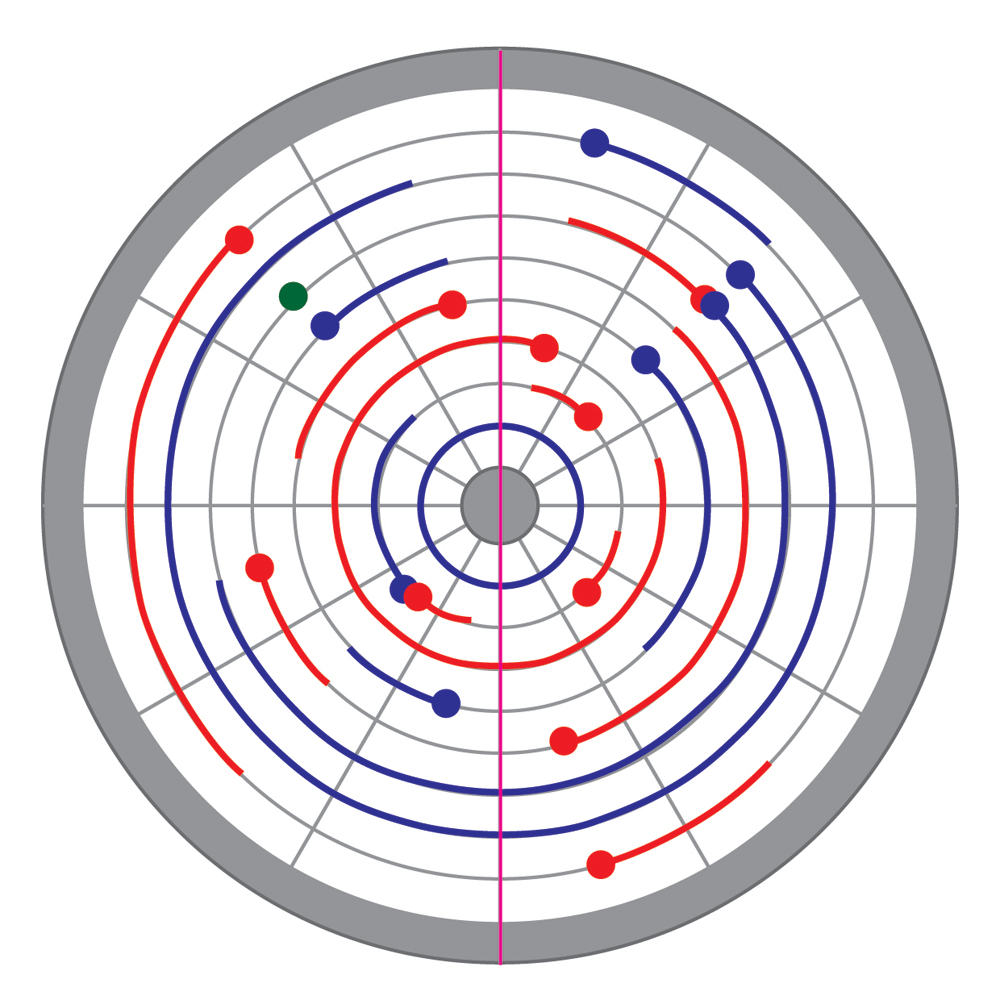
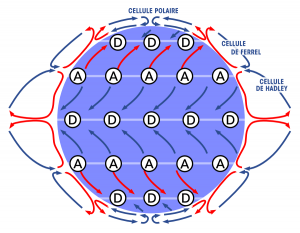
A mes yeux, cette ronde fluide semble figurer des courants atmosphériques circulant autour du globe. Et si le Crop Circle de Wilton Windmill représentait en réalité notre planète vue à partir du pôle nord ?
Deux éléments viennent supporter cette hypothèse. Le premier tient aux cellules atmosphérique qui caractérisent la formation des zones de hautes et de basses pressions autour du globe : Du pôle à l’équateur, on trouve dans l’ordre la cellule polaire, la cellule de Ferrel et la cellule de Hadley, au sein desquelles le sens de rotation de l’air s’inverse successivement.
La même inversion des « courants » est figurée dans notre Crop Circle : Ils se déplacent majoritairement de façon dextrogyre (dans le sens des aiguilles d’une montre) entre les 2e et 5e cercles intermédiaires puis de manière résolument levogyre au-delà de la 6ème enceinte.
Or c’est précisément sur cette 6ème enceinte que figure notre « anomalie » du chiffre 3 isolé. Sachant que la cellule de Ferrel s’étend du 30e au 60e parallèle environ et qu’elle joue un rôle d’échangeur entre les deux courants d’altitude que sont le courant polaire et le courant subtropical, nous ne devrions pas être si surpris de retrouver notre anomalie à la hauteur… du 60e parallèle, précisément à l’aplomb de la zone du courant polaire.
Alors que l’année 2010 n’avait pas encore atteint le solstice d’été, l’apparition du Crop Circle de Wilton Windmill nous invitait peut-être à porter une attention particulière aux changements atmosphérique en cours et à leurs futures conséquences, et pour cause :
…2010 se préparait à battre un nouveau record de chaleur, égalant l’anomalie de chaleur de 2005. Il y a fort à craindre du reste que 2014 ne les relègue d’ici peu à la deuxième place.
Ce postulat de lecture du Crop Circle de Wilton Windmill semble donc plus que jamais d’actualité. S’il s’avère correct, il se pourrait que quelque chose de fâcheux se produise au niveau de la dynamique du front polaire.
Pour illustrer les conséquences possibles d’une fluctuation importante de l’oscillation arctique, penchons-nous donc un instant sur cet article paru le 12 Janvier 2010, dans l’édition suisse du 20Minutes :
Personne n’est prophète en son pays…
Au-delà de leur réalisation mystérieuse, de leur beauté intrinsèque et des postulats de lecture qui peuvent diviser les esprits les plus ouverts à leur authenticité, il me paraît important de prendre le temps de réfléchir à l’intention qui sous-tend leur apparition.
Ma conviction est qu’ils constituent une forme de communication visant à susciter une prise de conscience, attirer notre attention ou stimuler notre réflexion sur une variété de sujets. A cet égard, l’énonciation incorrecte d’un théorème mathématique connu depuis deux siècles pour la seule beauté de sa formulation m’apparaît comme un pur gaspillage.
Pour celles et ceux qui souhaitent se faire une opinion sur la question, je recommande pour ma part le magnifique ouvrage de Rémy Wenger paru aux Editions Chaman.